深度优先搜索模板 (深度优先搜索的时间复杂度)

文章编号：39297 更新时间：2025-01-05 分类：互联网资讯 阅读次数：次

资讯内容

深度优先搜索模板与复杂度分析深度优先搜索的时间复杂度

一、引言

在计算机科学中，深度优先搜索（Depth-First Search，DFS）是一种用于遍历或搜索树或图的算法。
这种方法遵循一种策略，即沿着树的深度遍历树的节点，尽可能深地搜索树的分支。
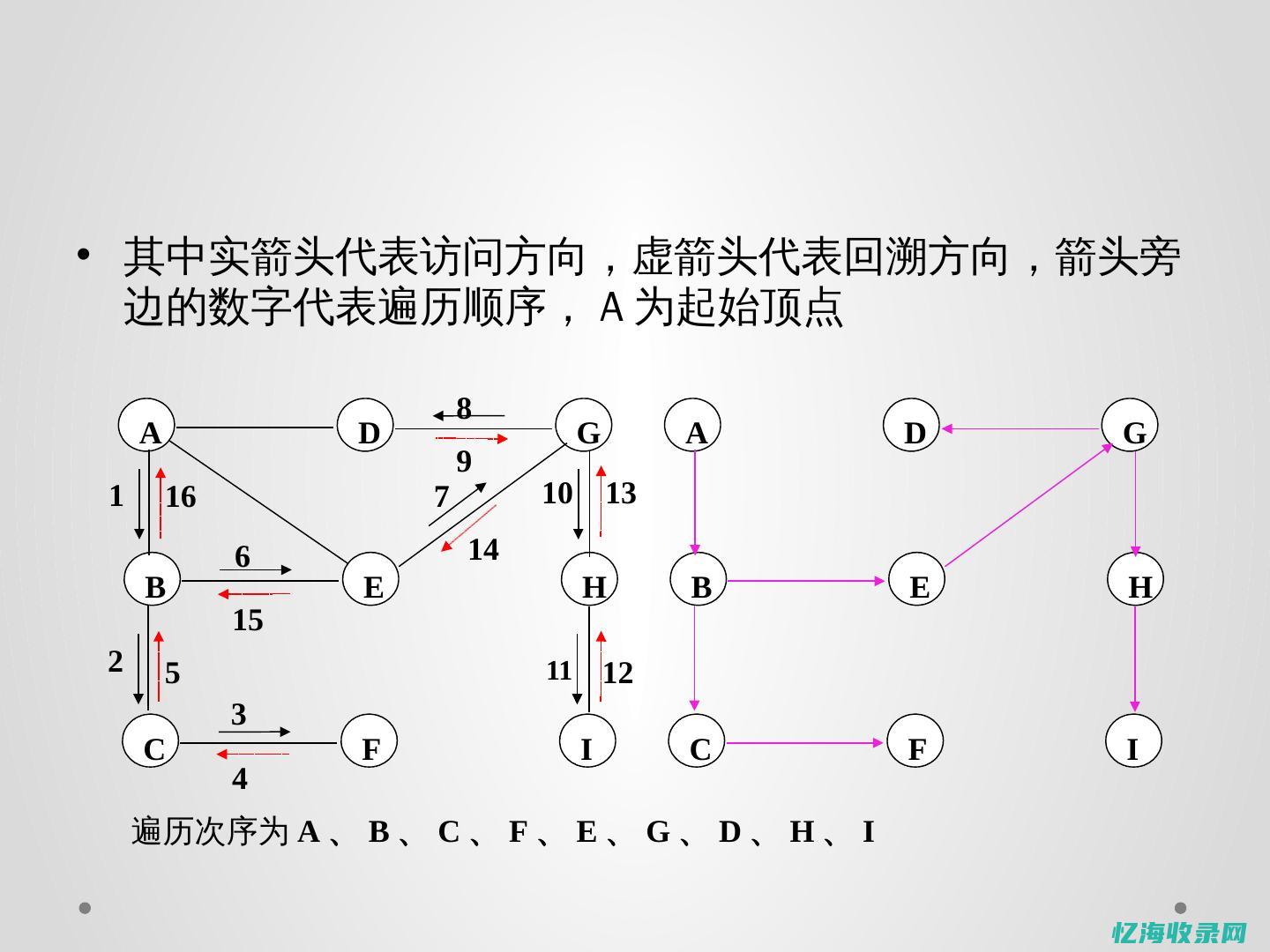
当到达树的末端时，它会回溯并继续探索其他路径。深度优先搜索模板
深度优先搜索通常适用于查找连通性问题，例如在迷宫中寻找路径等场景。
本文将介绍深度优先搜索的基本模板，并分析其时间复杂度。

二、深度优先搜索模板

深度优先搜索通常可以用递归实现，下面是一个简单的模板代码（以Python为例）：

```python
def dfs(graph, start):
visited = set() 记录已访问过的节点
path = [] 记录当前路径
dfs_util(graph, start, visited, path) 从起始节点开始深度优先搜索
return path 返回找到的路径或结果

def dfs_util(graph, node, visited, path):
path.append(node) 添加当前节点到路径中
visited.add(node) 标记当前节点为已访问
for next in graph[node]: 遍历当前节点的邻居节点
if next notin visited: 如果邻居节点未被访问过，则继续深入搜索
dfs_util(graph, next, visited, path) 递归调用dfs_util函数进行深度优先搜索
```
在这个模板中，我们首先定义一个`dfs`函数作为入口点，它接受一个图和一个起始节点作为输入。我们使用一个递归函数`dfs_util`来实现深度优先搜索的核心逻辑。模板还包括两个辅助集合`visited`和`path`，分别用于记录已访问的节点和当前路径。通过递归调用`dfs_util`函数，我们可以沿着图的边进行深度优先遍历。每次调用函数时，我们首先将当前节点添加到路径中并将其标记为已访问，然后遍历当前节点的邻居节点。如果邻居节点未被访问过，我们递归地调用`dfs_util`函数进行进一步的搜索。通过这种方式，我们可以找到从起始节点到目标节点的路径。如果无法找到目标节点或到达图的末尾时，回溯并继续探索其他路径。最后返回找到的路径或结果。在实际应用中，我们可以根据问题的需求修改模板代码以适应不同的场景。例如，我们可以添加条件判断来处理特定的约束条件或添加其他数据结构来存储中间结果等。三、深度优先搜索的时间复杂度分析深度优先搜索的时间复杂度取决于图的结构和大小。在理想情况下，如果图是一个平衡树结构（例如二叉树），深度优先搜索的时间复杂度为O(n)，其中n是图中的节点数量。在这种情况下，每个节点仅被访问一次且仅处理一次。在实际应用中，图的结构往往是不规则的，可能存在大量的分支和复杂的连通性。在这种情况下，深度优先搜索的时间复杂度可能会更高。最坏情况下，如果图是高度不平衡的或者存在大量的循环依赖关系，时间复杂度可能达到O(n!)，这可能导致算法效率较低且无法在可接受的时间内找到解。空间复杂度也是一个需要考虑的因素。深度优先搜索需要存储已访问的节点和当前路径等数据结构，因此空间复杂度取决于存储这些数据结构所需的内存大小。通常情况下，空间复杂度也是O(n)。但是具体的空间复杂度还取决于图的结构和算法的实现方式等因素。因此在实际应用中需要根据具体情况进行优化和调整算法以提高效率。四、总结本文介绍了深度优先搜索的基本模板并分析了其时间复杂度。深度优先搜索是一种适用于遍历或搜索树或图的算法它通过沿着图的深度遍历树的节点尽可能深地搜索树的分支以找到目标节点或路径。在实际应用中需要根据问题的需求和图的结构进行调整和优化以提高算法的效率。同时还需要考虑空间复杂度等因素以确保算法能够在有限的资源内运行并得到正确的结果。

在用邻接表表示图时,对图进行深度优先搜索遍历的算法的时间复杂度为()

因为当相邻矩阵的大部分被破坏时，矩阵中的所有元素都需要扫并追踪到，且元素个数为n＾2，自然算法为O（n＾2）。

所以邻接表只存储边或弧，如果扫描邻接表，当然会得到O（n＋e）其中n是顶点的数量，e的边或弧的数量。

设有n个点，e条边

邻接矩阵：矩阵包含n＾2个元素，在算法中共n个顶点，对每个顶点都要遍历n次，所以时间复杂度为O（n＾2）。

邻接表：包含n个头结点和e个表结点，算法中对所有结点都要遍历一次，所以时间复杂度为O（n+e）顺便，对于广度优先算法的时间复杂度，也是这样。

扩展资料：

邻接表是图的最重要的存储结构之一，描述了图上的每个点。创建一个容器对于每一个图的顶点（n顶点n容器）和节点在第i个容器包含所有相邻顶点的顶点Vi。事实上，我们经常使用的邻接矩阵是一个邻接表的边集不离散化每一个点。

在有向图中，描述每个点与另一个节点连接的边(在a点->点B)。

在无向图中，描述每个点上的所有边（A点和B点的情况）

邻接表对应的图存储方法称为边集表。此方法将所有边存储在容器中。

经典搜索算法总结

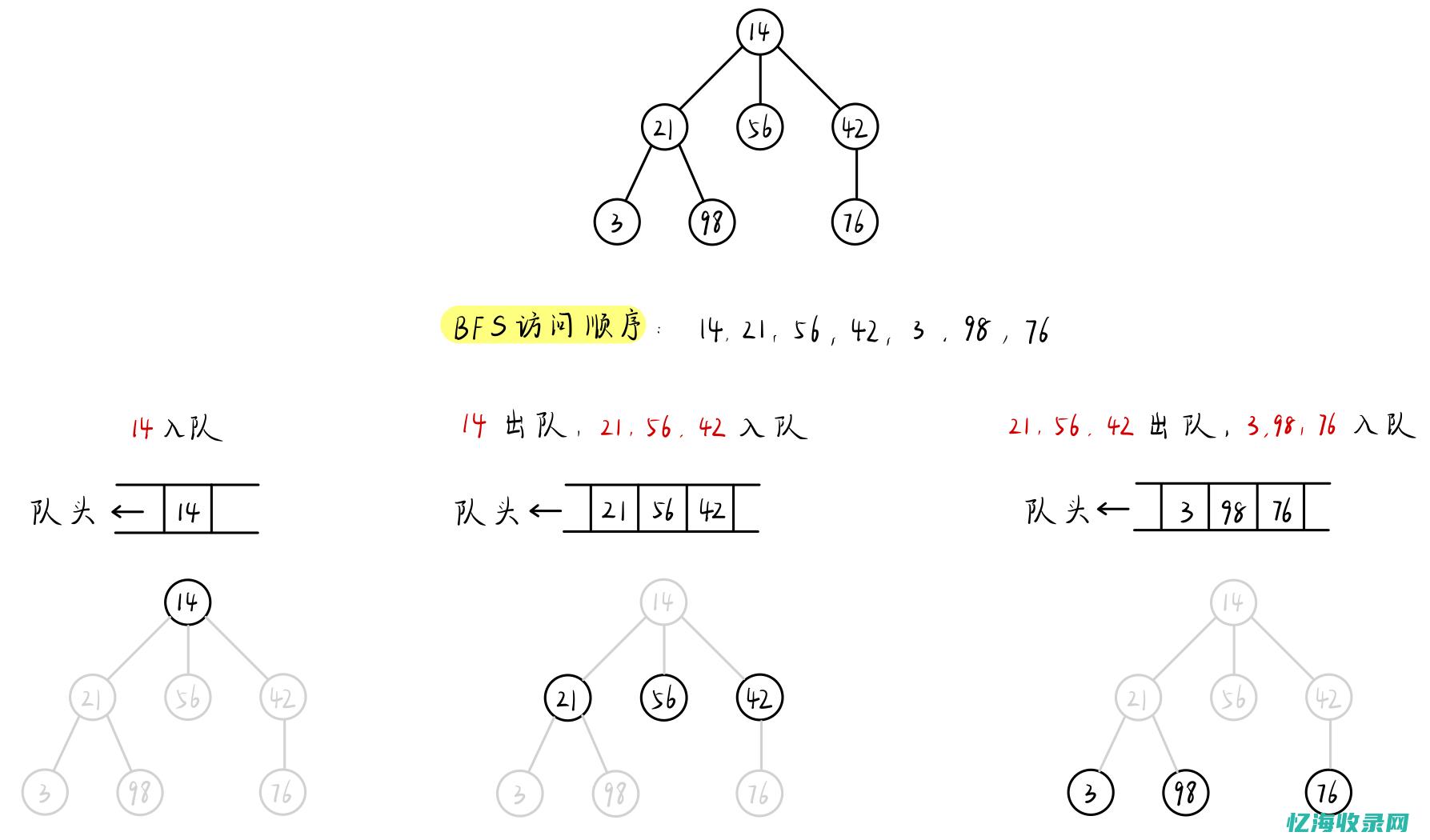
在人工智能的探索之旅中，我们邂逅了众多精妙的搜索算法，它们如同璀璨的星辰，照亮了我们在复杂问题求解中的道路。让我们聚焦于两大核心类别：无信息搜索（BFS）与有信息搜索（UCS，包括A*搜索），以及它们各自独特的魅力和特性。首先，无信息搜索中的BFS（宽度优先搜索）就像一个耐心的探索者，它用FIFO队列小心翼翼地拓展边界，确保在有限深度下找到潜在的最佳解。然而，它的前提是问题结构允许，否则可能无法触及最优。相比之下，UCS（统一代价搜索）通过优先队列，犹如一位智慧的导航者，探寻最短路径，确保了高效性和方向性。深入探讨，状态的定义至关重要，它包含了决策者所需的所有关键信息，以选择出未来的最佳行动。在这个框架下，UCS与Dijkstra算法有所区别，后者更侧重于精确度，但缺乏UCS的灵活性和启发式指导。 DFS（深度优先搜索）和BFS形成了鲜明对比。 DFS利用栈来维护frontier，虽然在树搜索中容易陷入无穷循环，但在图搜索中却大显身手，尽管时间复杂度较高，空间需求却相对较低。深度受限的DFS（DLS）和迭代加深搜索（IDS）则是对深度的限制进行细化，优化了搜索策略。双向搜索（BS）将BFS的效率和深度优先搜索的探索性结合，时间与空间复杂度与BFS持平，但提供了额外的搜索维度。而启发式搜索，如贪心搜索，依赖于额外的信息，尽管不能保证全局最优，但在特定场景下能显著减少无效探索。 A*搜索则是在UCS的基础上，引入了启发式评估函数，admissibility与consistency的黄金法则，使得搜索更加高效，尽管它可能需要遍历更多节点，但其优点在于搜索范围的精确控制。 RBFS算法巧妙地结合了递归和循环，通过successor队列优化，平衡了效率与递归特性。新子递归算法的引入，提高了效率，当successor节点超过特定阈值时，算法会选择最优节点进行扩展。然而，这牺牲了部分即时性，但空间节省是其显著优势。启发式评估在搜索中扮演了重要角色，如8-puzzle问题，通过启发式评估，平均宽度减小，探索状态数量大幅减少。设计启发式时，务必满足admissible和consistent，确保搜索的正确性和有效性。最后，衡量启发式好坏的b*指标，强调了深度相关性，而非绝对节点数。相比于单纯依赖节点数，这为我们提供了更全面的评估视角。生成启发式的方法包括基于问题放松、子问题模式数据库和经验学习，而多种admissible heuristics的结合，往往能带来更佳的搜索性能。总的来说，这些搜索算法犹如一套独特的工具箱，根据问题的特性与需求，选择最合适的工具，才能在人工智能的探索道路上行稳致远。