深度优先搜索(Depth-First Search,简称DFS)是图遍历的一种算法。
它沿着树的深度遍历树的节点,尽可能深地搜索树的分支。
本文将详细介绍深度优先搜索的顺序,并给出具体算法模板。
在此基础上,结合实际例子进一步说明其实现过程,最后对深度优先搜索进行小结。
1. 选择一个起始节点,将其标记为已访问。
2. 从起始节点出发,访问其所有未被访问过的邻居节点。对于每个邻居节点,按照深度优先搜索的顺序进行递归访问。
3. 若所有邻居节点均已被访问,回溯到上一层节点,继续访问其未被访问过的邻居节点。
4. 重复步骤3,直到所有节点均被访问过。
这种搜索顺序的关键在于使用递归的思想来实现对树或图的深度遍历。
当当前节点的所有邻居节点都被访问过后,回溯到上一层节点继续访问其未被访问过的邻居节点。
通过这种方式,可以确保每个节点都被访问一次。
```python
def dfs(graph, start):
visited = set() 存储已访问过的节点
stack = [start] 存储待访问的节点,采用栈结构进行存储和取出操作
while stack: 如果栈不为空,继续搜索
vertex = stack.pop() 弹出栈顶元素进行访问
if vertex not in visited: 如果该节点未被访问过
visited.add(vertex) 将其标记为已访问
stack.extend(graph[vertex] - visited) 将该节点的邻居节点加入栈中等待后续访问
returnvisited 返回所有已访问的节点集合
```
四、深度优先搜索实现过程示例
A --> B -->D --> E --> F --> G --> H --> I --> J --> K --> L --> M --> N --> O --> P --> Q --> R -->S --> T --> U --> V --> W --> X --> Y --> Z (箭头表示连接关系)这是一个简单的链表结构图。
我们可以使用深度优先搜索算法遍历这个图的所有节点。
以节点A作为起始点进行深度优先搜索的过程如下:首先访问节点A,然后依次访问节点B、D、E等相邻节点。
当无法继续向更深的方向移动时,回溯到上一层节点继续访问相邻节点。
如此反复,直到所有节点都被访问过为止。
具体的实现过程可以根据算法模板进行编程实现。
这里不再赘述。
需要注意的是,在实际应用中,图的结构可能更加复杂,需要根据具体情况进行相应的调整和优化。
在复杂图的情况下,通常还需要结合其他技术(如剪枝)以提高算法的效率和稳定性。
实际应用中可能还需要处理一些特殊情况(如死循环等问题),这些都需要根据实际情况进行灵活处理。
五、总结本文详细介绍了深度优先搜索的顺序和算法模板,并结合实际例子说明了实现过程。
通过了解深度优先搜索的基本概念和原理,可以更好地理解和应用这种算法思想。
在实际应用中,深度优先搜索不仅可以用于遍历图或树的结构,还可以应用于解决许多问题(如路径问题、最短路径问题等)。
在实际使用时需要结合具体情况进行优化和调整以实现更好的效果。
在实际应用中遇到的困难和挑战也可以通过不断地学习和实践来解决和提高自己的水平。
希望本文能够帮助读者更好地理解深度优先搜索算法并能在实际应用中发挥积极的作用。
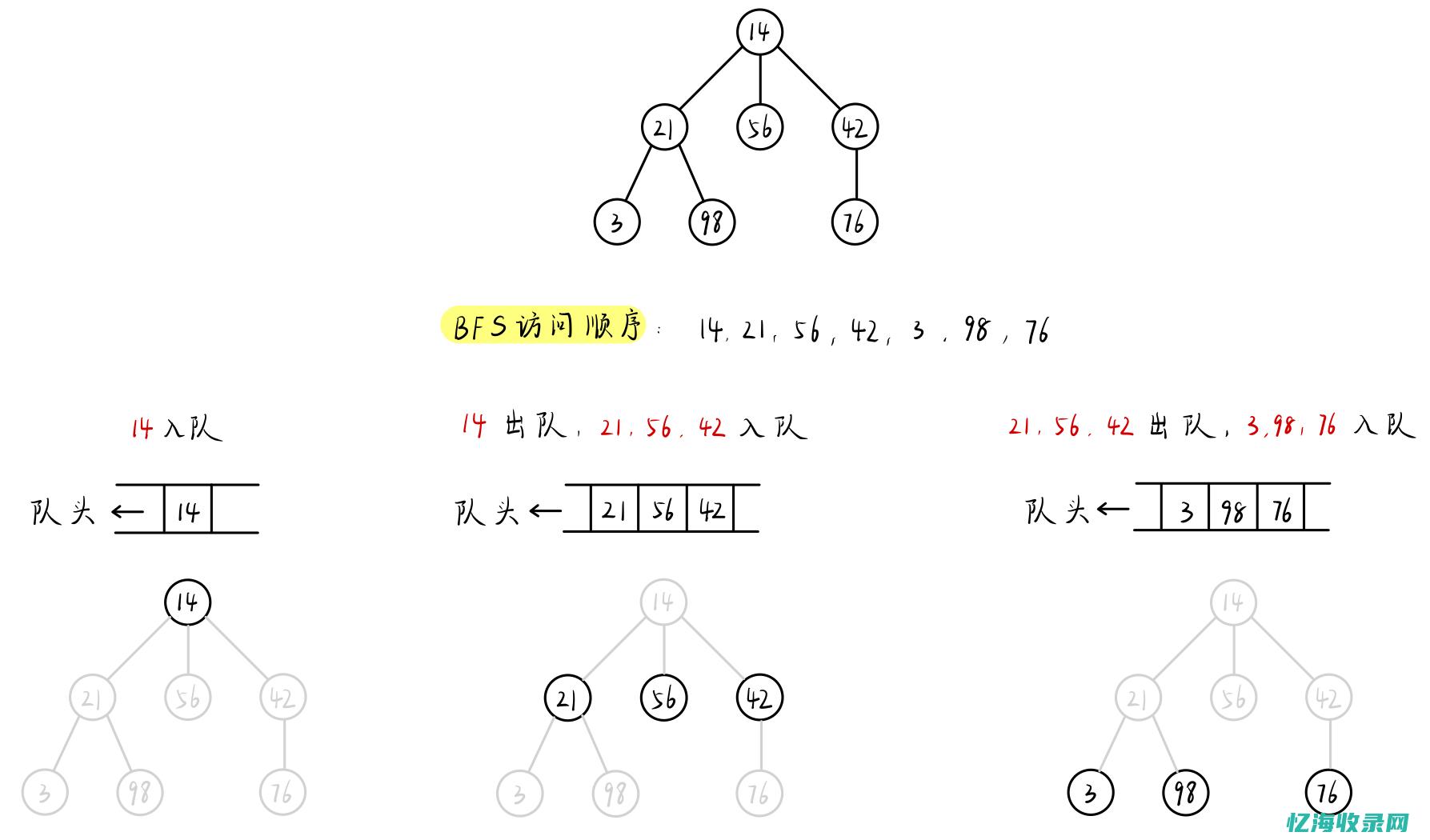
深度优先遍历和广度优先遍历对比是搜索顺序不同、操作步骤不同。
1、搜索顺序不同
广度优先搜索会根据离起点的距离,按照从近到远的顺序对各节点进行搜索。 而深度优先搜索会沿着一条路径不断往下搜索直到不能再继续为止,然后再折返,开始搜索下一条路径。
在深度优先搜索中,保存候补节点是栈,栈的性质就是先进后出,即最先进入该栈的候补节点就最后进行搜索。 深度优先搜索会沿着一条路径不断往下,搜索直到不能再继续为止,到了路径的尽头,再折返,再对另一条路径进行搜索。
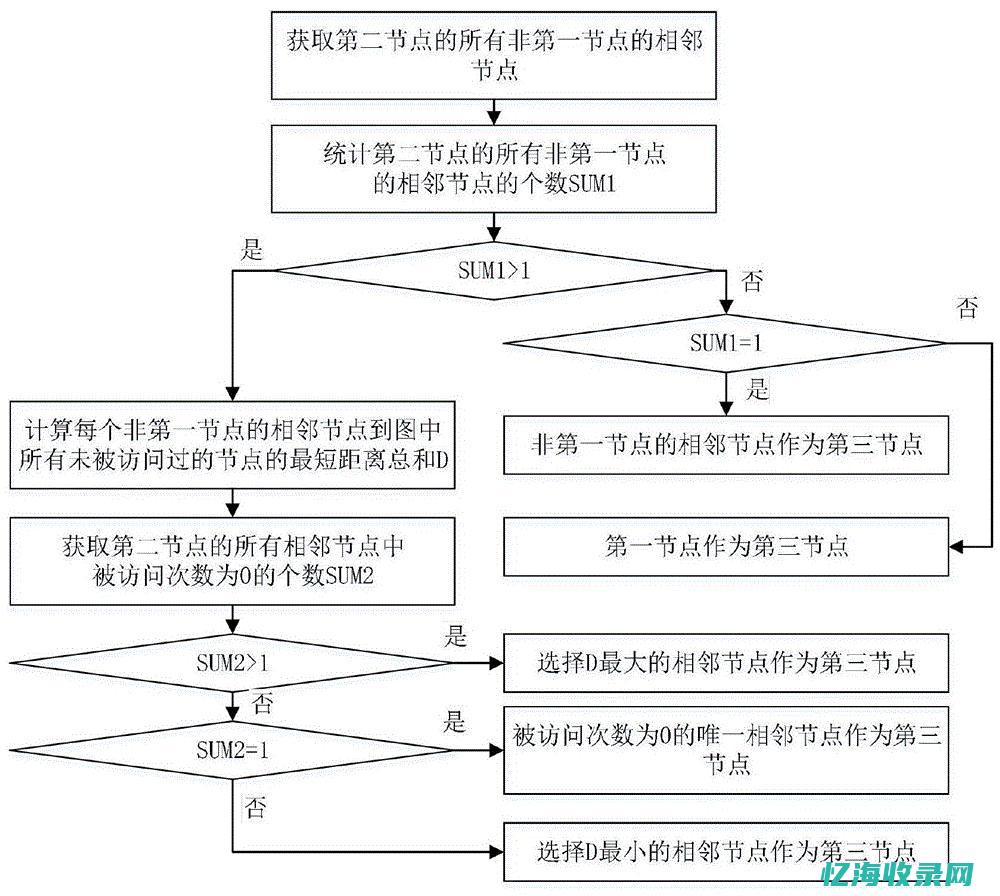
2、操作步骤不同
虽然广度优先搜索和深度优先搜索在搜索顺序上有很大的差异,但是在操作步骤上却只有一点不同,那就是选择哪一个候补节点作为下一个节点的基准不同。
广度优先搜索选择的是最早成为候补的节点,因为节点离起点越近就越早成为候补,所以会从离起点近的地方开始按顺序搜索;而深度优先搜索选择的则是最新成为候补的节点,所以会一路往下,沿着新发现的路径不断深入搜索。
搜索引擎基本工作原理简述
搜索引擎为了以最快的速度得到搜索结果,它搜索的内容通常是预先整理好的网页索引数据库。 普通搜索,不能真正理解网页上的内容,它只能机械地匹配网页上的文字。 真正意义上的搜索引擎,通常指的是收集了互联网上几千万到几十亿个网页并对网页中的每一个文字(即关键词)进行索引,建立索引数据库的全文搜索引擎。
当用户查找某个关键词的时候,所有在页面内容中包含了该关键词的网页都将作为搜索结果被搜出来。 在经过复杂的算法进行排序后,这些结果将按照与搜索关键词的相关度高低,依次排列。
深度优先搜索(DFS)是一种遍历算法,常用于解决与图相关的问题。 从起始节点开始,沿着路径尽可能深入,直到无法继续,回溯后探索其他路径,直至遍历完整个图。 DFS核心思想在于深度优先遍历图或树的节点。 从一个起始点出发,沿路径深入节点,直至无法前进时回溯,继续探索其他路径。 此过程重复直至图或树遍历完毕。 DFS基本步骤包括:确定“满足条件”、执行“对应操作”、评估“判断边界”、设定“遍历条件”。 调整填写这些部分,可应用于各种DFS相关问题。 图解示例:从节点A开始遍历,按照深度优先原则深入每个路径直至终点,回溯后继续探索,直至遍历完整个图。 DFS广泛用于图遍历和解决特定问题,如全排列、八皇后、组合问题等。 学习DFS,通过模拟实现过程并实践,能更深刻理解算法。 常见练习题包括全排列、八皇后和组合问题。 DFS算法是解决复杂问题的重要工具,适用于多种场景。 总结,理解DFS的关键在于实际操作和应用。 通过刷题和解决具体问题,能熟练掌握DFS,进一步深入算法学习。 希望提供的例子能帮助你更好地理解和运用DFS算法。 如有更多疑问,欢迎提问或留言。 感谢阅读。
深度优先搜索(DFS)和广度优先搜索(BFS)是两种常用的图形搜索算法,它们在原理上虽有相似之处,但在应用和执行方式上存在差异。 以下是对这两种算法的详细解析:一、深度优先搜索(DFS)深度优先搜索是一种图论中的经典算法,它采用深度优先的方法遍历或搜索树或图。 该算法常用于解决图论问题,如拓扑排序和路径问题。 DFS通过递归或栈来实现,确保每个节点只被访问一次。 其搜索过程是先深入一个分支,直到该分支的最后一个节点,然后回溯至最近的分叉点继续搜索其他分支。 基本步骤:1. 从根节点开始,按照左分枝优先的原则,将节点按顺序压入栈中。 2. 访问栈顶节点,并标记为已访问。 3. 查找与当前节点相邻且未被访问的节点,并将其压入栈中。 4. 如果当前节点没有未访问的邻接点,则从栈中弹出该节点,并重复步骤3。 5. 直到所有节点都被访问,算法结束。 二、广度优先搜索(BFS)广度优先搜索是一种优先遍历图形中所有相邻节点的算法。 它从根节点开始,按层次遍历树的节点,直到找到所需结果。 BFS使用队列数据结构来存储待访问的节点。 基本步骤:1. 对给定的连通图进行初始化,所有节点标记为未访问。 2. 将起点节点标记为灰色,即待访问状态。 3. 访问灰色节点,并将其标记为黑色,即已访问。 4. 将灰色节点的所有未被访问的邻接点标记为灰色,并加入队列。 5. 从队列中取出灰色节点,并重复步骤3和4,直到目标节点被访问。 6. 算法结束,可得到从起点到终点的最短路径。 通过以上解析,我们可以看到DFS和BFS在搜索过程中的不同策略。 DFS更加深入地遍历图的分支,而BFS则按层次遍历。 这两种算法在实际应用中各有优势,根据具体问题和需求选择合适的搜索算法。
标签: 深度优先搜索顺序、 深度优先搜索模板、本文地址: https://yihaiquanyi.com/article/c2a377b1864409a2352e.html
上一篇:seo诊断工具有哪些seo诊断...