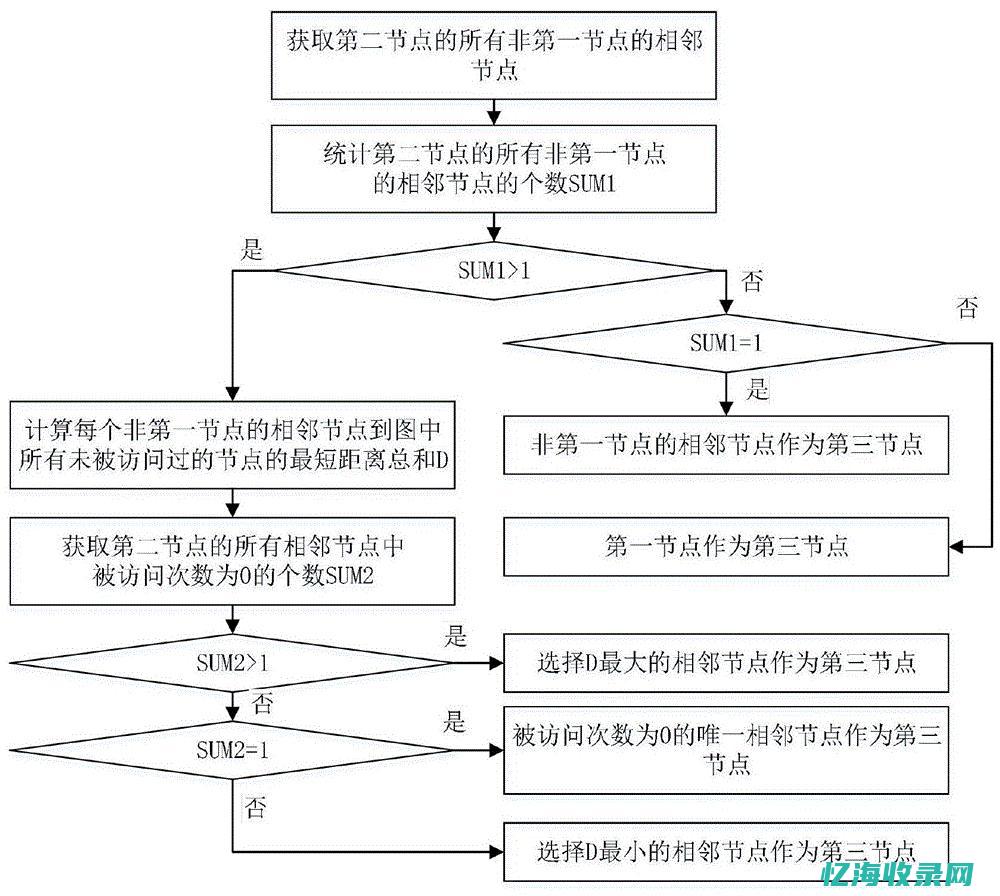
在计算机科学领域中,搜索算法是研究和解决实际问题的一种重要手段。
其中,深度优先搜索(Depth-First Search,简称DFS)和广度优先搜索(Breadth-First Search,简称BFS)是两种常见的搜索策略。
本文将对深度优先搜索进行详细介绍,并将其与广度优先搜索进行对比,以便更好地理解这两种搜索算法的特点和适用场景。
深度优先搜索是一种用于遍历或搜索树或图的算法。
该算法会尽可能深地搜索树的分支,当节点v的所在边都已被探寻过,搜索将回溯到发现节点v的那条边的起始节点。
这一过程一直进行到已发现从源节点可达的所有节点为止。
如果还存在未被发现的节点,则选择其中一个作为源节点并继续搜索。
深度优先搜索可以使用栈(Stack)来实现。具体步骤如下:
1. 从根(或任意节点)出发,访问该节点。
2. 将该节点的所有未访问的邻居节点加入栈中。
3. 弹出栈顶节点,访问之。
4. 将弹出节点的所有未访问的邻居节点加入栈中。
5. 重复步骤3和4,直到所有节点都被访问过。
1. 当需要找到从起点到终点的最短路径时,深度优先搜索可以作为一个很好的起点。尽管它不能保证找到最短路径,但在许多情况下都能找到有效路径。
2. 当需要遍历整个图或树以获取所有节点的信息时,深度优先搜索也是一个很好的选择。它可以确保遍历所有可达节点。
广度优先搜索是另一种用于遍历或搜索图或树的算法。
与深度优先搜索不同,广度优先搜索会从根(或任意节点)出发,首先探索离根最近的节点,然后再逐层向下探索。
广度优先搜索使用队列(Queue)来实现。
1. 从根(或任意节点)出发,访问该节点。
2. 将该节点的所有未访问的邻居节点加入队列中。
3. 从队列中取出一个节点,访问之。
4. 将该节点的所有未访问的邻居节点加入队列中。
5. 重复步骤3和4,直到所有节点都被访问过。
1. 当需要找到从起点到终点的最短路径时,广度优先搜索是最优选择。因为它总是先探索离起点最近的节点,所以能够确保找到最短路径。
2. 在需要遍历整个图以获取特定信息时,广度优先搜索也是一个很好的选择。例如,在图中的每个节点都需要被处理一次的情况下,广度优先搜索可以确保节点的处理顺序是按照它们离起点的距离来决定的。
1. 算法实现:深度优先搜索使用栈来记录待访问的节点,而广度优先搜索使用队列。这两种数据结构在处理节点的顺序上有所不同,导致算法的行为差异。
2. 适用场景:深度优先搜索更适用于寻找最短路径的起始阶段或者遍历整个图/树的情况;而广度优先搜索更适用于寻找最短路径和确保节点处理顺序的情况。在某些特定场景下,如存在环路的情况,广度优先搜索可能会导致无限循环,而深度优先搜索则可以通过回溯机制避免这一问题。
3. 时间复杂度:在大多数情况下,深度优先搜索的时间复杂度为O(V+E),其中V是顶点数,E是边数。而广度优先搜索的时间复杂度也大致相同。在实际应用中,由于实现方式和具体场景的差异,时间复杂度可能会有所不同。
总结:深度优先搜索和广度优先搜索是两种重要的搜索策略,各有其优点和适用场景。
在实际应用中,应根据具体需求和场景选择合适的搜索算法。
一、指代不同
1、深度优先遍历:是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。
2、广度优先遍历:系统地展开并检查图中的所有节点,以找寻结果。
二、特点不同
1、深度优先遍历:所有的搜索算法从其最终的算法实现上来看,都可以划分成两个部分──控制结构和产生系统。 正如前面所说的,搜索算法简而言之就是穷举所有可能情况并找到合适的答案,所以最基本的问题就是罗列出所有可能的情况,这其实就是一种产生式系统。
2、广度优先遍历:并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
三、算法不同
1、深度优先遍历:把根节点压入栈中。 每次从栈中弹出一个元素,搜索所有在它下一级的元素,把这些元素压入栈中。 并把这个元素记为它下一级元素的前驱。 找到所要找的元素时结束程序。 如果遍历整个树还没有找到,结束程序。
2、广度优先遍历:把根节点放到队列的末尾。 每次从队列的头部取出一个元素,查看这个元素所有的下一级元素,把它们放到队列的末尾。 并把这个元素记为它下一级元素的前驱。 找到所要找的元素时结束程序。 如果遍历整个树还没有找到,结束程序。
深度优先搜索(DFS)和广度优先搜索(BFS)是两种常用的图形搜索算法,它们在原理上虽有相似之处,但在应用和执行方式上存在差异。 以下是对这两种算法的详细解析:一、深度优先搜索(DFS)深度优先搜索是一种图论中的经典算法,它采用深度优先的方法遍历或搜索树或图。 该算法常用于解决图论问题,如拓扑排序和路径问题。 DFS通过递归或栈来实现,确保每个节点只被访问一次。 其搜索过程是先深入一个分支,直到该分支的最后一个节点,然后回溯至最近的分叉点继续搜索其他分支。 基本步骤:1. 从根节点开始,按照左分枝优先的原则,将节点按顺序压入栈中。 2. 访问栈顶节点,并标记为已访问。 3. 查找与当前节点相邻且未被访问的节点,并将其压入栈中。 4. 如果当前节点没有未访问的邻接点,则从栈中弹出该节点,并重复步骤3。 5. 直到所有节点都被访问,算法结束。 二、广度优先搜索(BFS)广度优先搜索是一种优先遍历图形中所有相邻节点的算法。 它从根节点开始,按层次遍历树的节点,直到找到所需结果。 BFS使用队列数据结构来存储待访问的节点。 基本步骤:1. 对给定的连通图进行初始化,所有节点标记为未访问。 2. 将起点节点标记为灰色,即待访问状态。 3. 访问灰色节点,并将其标记为黑色,即已访问。 4. 将灰色节点的所有未被访问的邻接点标记为灰色,并加入队列。 5. 从队列中取出灰色节点,并重复步骤3和4,直到目标节点被访问。 6. 算法结束,可得到从起点到终点的最短路径。 通过以上解析,我们可以看到DFS和BFS在搜索过程中的不同策略。 DFS更加深入地遍历图的分支,而BFS则按层次遍历。 这两种算法在实际应用中各有优势,根据具体问题和需求选择合适的搜索算法。
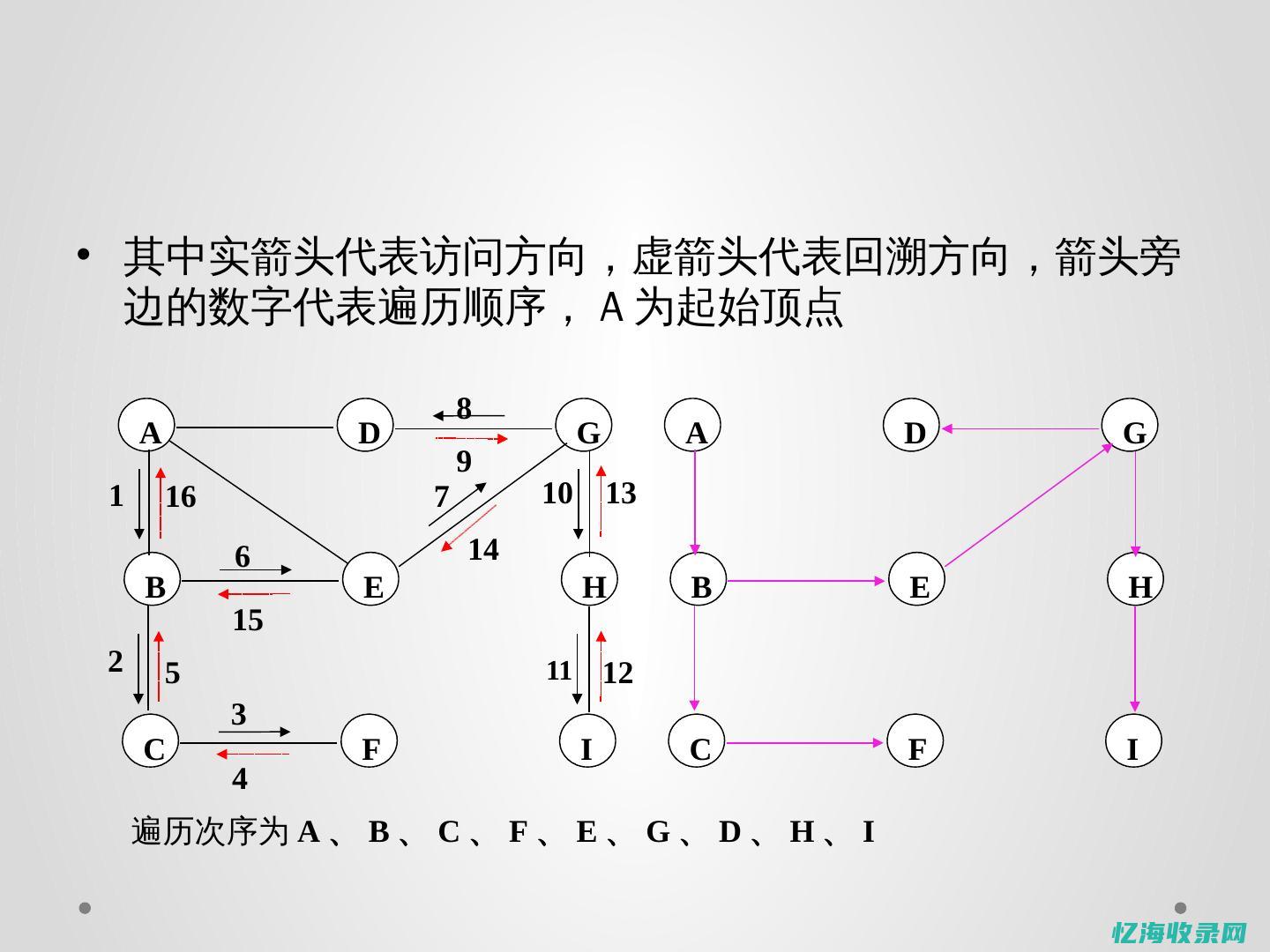
广度优先和深度优先的区别如下:
标签: 深度优先搜索和广度优先搜索对比、 深度优先搜索模板、本文地址: https://yihaiquanyi.com/article/def3dd7838192500ab34.html
上一篇:seo深度优化平台seo深度解析第二版pdf...